Research topics
Population Genetics and Evolution

Charles Darwin's 1837 sketch of an evolutionary tree
Deeper understanding of biological evolution requires quantitative prediction of the consequences of fundamental processes such as inheritance, mutation, recombination, migration, and selection. As in other natural sciences, mathematical models are essential for this purpose. Already some 100 years ago, the first basic models were developed to explain Darwin's theory of evolution using Mendel's theory of inheritance. The field that studies this interaction of genetic, ecological and evolutionary mechanisms is called population genetics. Animal and plant breeding, and more recently human medicine, are the main areas of practical application.
There are two complementary but interrelated approaches for the study of evolution. In the first, evolutionary processes, i.e. the temporal changes of traits or gene frequencies, are assessed for given assumptions about genetic mechanisms and forms of selection. Mathematically, this is done using differential equations, difference equations, or stochastic processes. In the second approach, one starts from real data representing the genetic composition of living species. With modern sequencing methods, it is possible to sequence whole genomes of hundreds or thousands of individuals of a population. The primary interest is in the differences in DNA sequences between individuals, called polymorphisms. From the patterns in these polymorphisms along the genome, one can infer evolutionary processes in the history of species (e.g., which ones are most closely related and how long ago the separation occurred, whether a population underwent phases of massive growth or contraction, or which genes are adaptive and have recently become established in a population by positive selection). Once again, stochastic processes are the main mathematical tool, complemented by statistical methods.
Kinetic theory
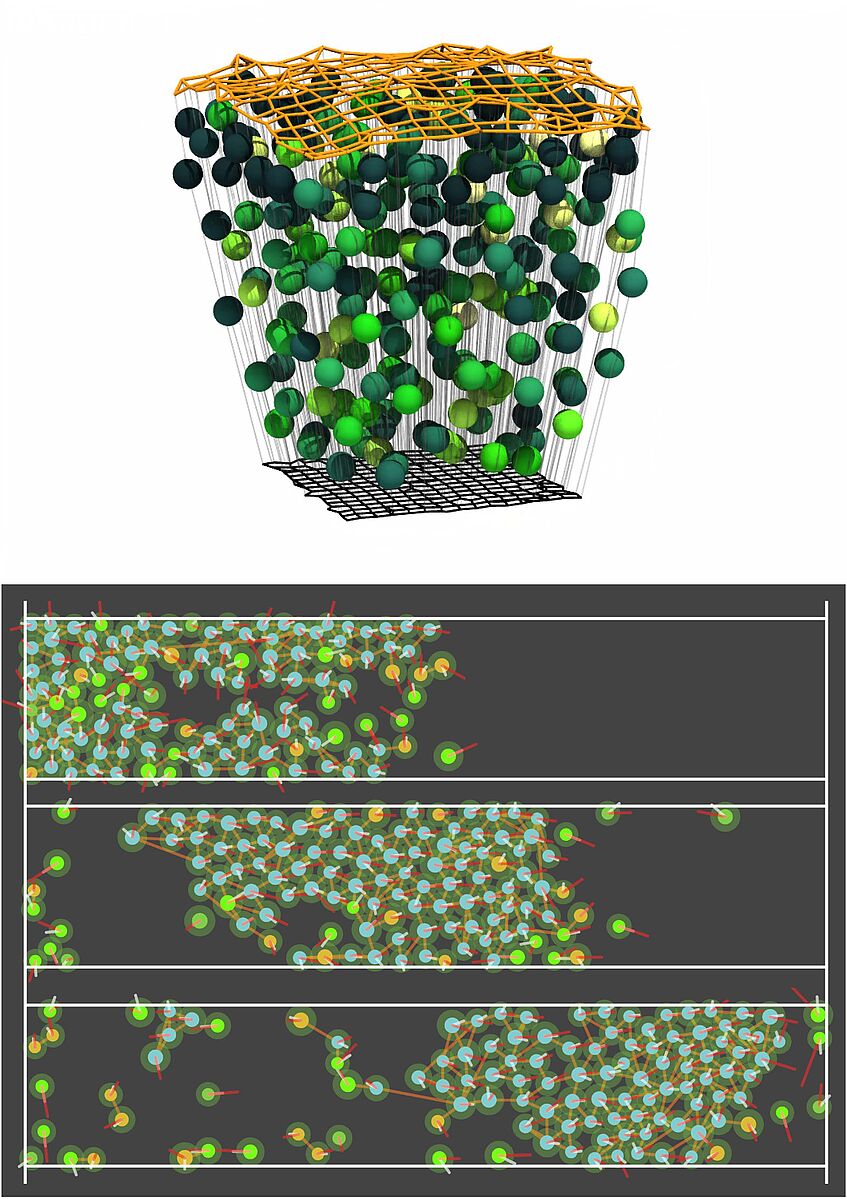
3D simulation of epithelial tissue and collective motion of cells in a confined domain (Steffen Plunder)
Kinetic theory provides powerful tools to study how macroscopic phenomena (observable patterns and dynamics) emerge from the underlying microscopic dynamics. Coarse-graining, i.e., the rigorous mathematical derivation of macroscopic equations from microscopic ones is the central theme of kinetic theory as kinetic equations provide an essential step between micro and macroscopic models. This process involves the analysis of partial differential equations and aims at the development of
efficient numerical methods for the macroscopic equations, as numerical simulations of the microscopic dynamics become inefficient when the number of particles is large.
Importantly, thanks to coarse-graining techniques, mathematics plays a central and unique role in science: it is the only known tool to establish a rigorous bridge across scales. Most current approaches in the biological sciences are based on modelling either at large scales or at small scales. Linking scales means establishing relations between knowledge gained at the different scales, in particular, how large-scale patterns arise from underlying lower-scale phenomena. Multi-scale phenomena are omnipresent in nature and its understanding is of paramount importance to explaining natural processes.
PDE models of cell movement
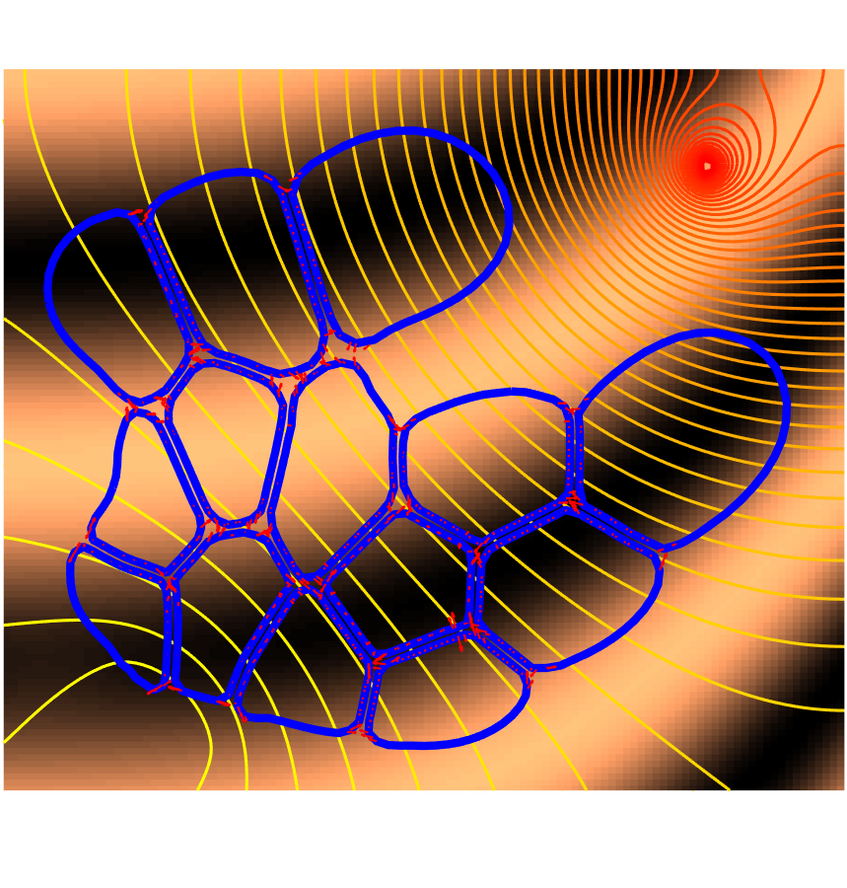
The crawling motion of many cell types is based on the lamellipodium, a flat cell protrusion supported by a network of actin filaments. The Filament Based Lamellipodium Model (FBLM) is a two-dimensional continuum model for the chemo-mechanics of the lamellipodium, including descriptions of the homeostatic balance of filament polymerization and depolymerization, the dynamics of cross-linking and substrate adhesions, the mechanical response to cell membrane stretching, and more.
The figure shows a snapshot from a simulation of a cluster of 14 cells described by the FBLM, incorporating the effects of a chemotactic signal (level sets in yellow and red), of a substrate with varying adhesiveness (darkness of the background), and of cell-cell adhesion (red arrows).
